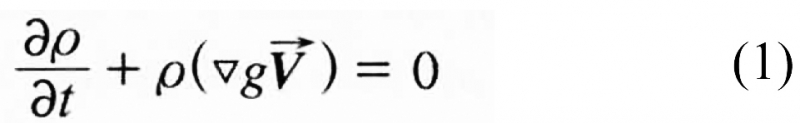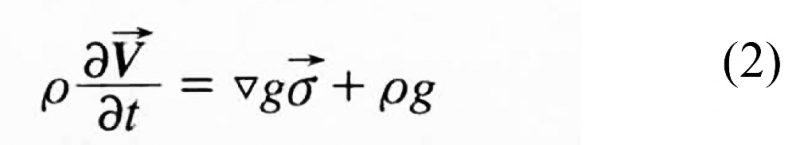付麗,薛平,劉麗超,賈明印
(北京化工大學機電工程學院,北京100029)
摘要:以熔融紡絲過程為研究對象,采用PTT本構模型,運用有限元分析方法,對高密度聚乙烯(PE-HD)改性超高分子量聚乙烯(PE-UHMW)共混物熔融法擠出初生絲的過程進行了數(shù)值模擬,對比分析了口模溫度和熔體泵轉速的變化對擠出過程速度場和剪切速率場分布的影響,探究了影響初生絲擠出脹大現(xiàn)象的因素。研究表明,隨著擠出口模溫度的升高,初生絲擠出脹大現(xiàn)象明顯減弱,擠出脹大比從280℃的1.318降低到310℃的1.264。然而,隨著熔體泵轉速的增大,初生絲擠出脹大現(xiàn)象顯著增強,擠出脹大比由轉速為1r/min的1.258增大到5r/min的1.318。
關鍵詞:超高分子量聚乙烯纖維;共混改性;熔融紡絲;擠出脹大;數(shù)值模擬
中圖分類號:TS155.6 文獻標識碼:A 文章編號:1001-3539(2019)04-0053-06
超高分子量聚乙烯(PE-UHMW)纖維與碳纖維、芳綸纖維并稱為世界三大高性能纖維,其優(yōu)越的物理性能已使PE-UHMW纖維成為目前世界上比強度和比模量最高的纖維[1]。目前工業(yè)上主要采用凝膠紡絲法進行PE-UHMW纖維的生產,但是凝膠紡絲法工藝復雜,需要使用溶劑,成本高,易造成環(huán)境污染[2],而熔融紡絲法無需溶劑[3],工藝路線簡單,成本低[4],具有很好的發(fā)展前景。
近年來,利用熔融法生產PE-UHMW纖維的研究越來越受到人們的關注。甄萬清等[2]研究了納米蒙脫土(MMT)對PE-UHMW纖維性能的影響,并從晶格變化的角度分析了纖維性能發(fā)生變化的原因;鄭艷超等[5]則分析了不同聚烯烴改性材料對PE-UHMW纖維熱性能、力學性能及纖維取向度等性能的影響,王非[6]、A.K.Doufas等[7]也分別做了相關研究。聚合物在熔融紡絲過程中不可避免的會出現(xiàn)擠出脹大以及熔體破裂現(xiàn)象,許多文獻[8–12]利用Polyflow軟件探究了工藝參數(shù)對擠出加工過程中聚合物擠出脹大現(xiàn)象的影響,發(fā)現(xiàn)利用氣輔成型的方法可以有效減小擠出脹大現(xiàn)象;相應的擠出脹大現(xiàn)象對熔融紡絲過程的影響主要表現(xiàn)為得到的PE-UHMW初生絲的直徑大于口模直徑,二次拉伸之后制得的纖維尺寸也無法得到保障,這為加工生產帶來不可避免的困難。然而,目前針對紡絲過程中擠出脹大現(xiàn)象的模擬研究[13]比較少見,尤其是PE-UHMW熔融紡絲的過程;因此筆者利用Polyflow軟件進行數(shù)值模擬,對高密度聚乙烯(PE-HD)改性PE-UHMW共混物熔融紡絲過程中初生絲的擠出脹大現(xiàn)象進行分析研究。
1模型建立
1.1數(shù)學模型
根據PE-UHMW/PE-HD熔融紡絲過程中熔體在口模中的流動現(xiàn)象和特點,做出如下假設:
熔體不可壓縮;流動方式為穩(wěn)定的層流;忽略重力和慣性力的影響;熔體為黏彈性流體且等溫流動。
連續(xù)性方程:
式中:
——速度矢量;
ρ——密度;
V——哈密爾頓算子。
動量方程:
式中:
——應力矢量;
g——重力加速度。
1.2材料模型
材料模型主要反映的是共混物料流動過程中應力和應變之間的關系。模擬過程中只有真實的反應這兩者之間的關系,才能得到相對準確的模擬結果。此處采用PTT微分黏彈模型,因為該模型能夠定量地描述聚合物的剪切黏度和法向應力差,對于粘彈性流體的流動來說,額外應力張量分為黏彈性張量T1和牛頓分量T2,即T=T1+T2,其中牛頓分量T2=2η0D,其粘彈性分量T1計算方法如式(3)所示:
式中:η0——零切黏度;
η1——模型指定黏度系數(shù);
λ——松弛時間;
tr——張量微量;
η2——牛頓分量黏度系數(shù);
D——變形速率張量;
ξ——與剪切有關的材料參數(shù);
ε——與拉伸黏度有關的材料參數(shù);
V——下隨體時間導數(shù);
Δ——上隨體時間導數(shù)。
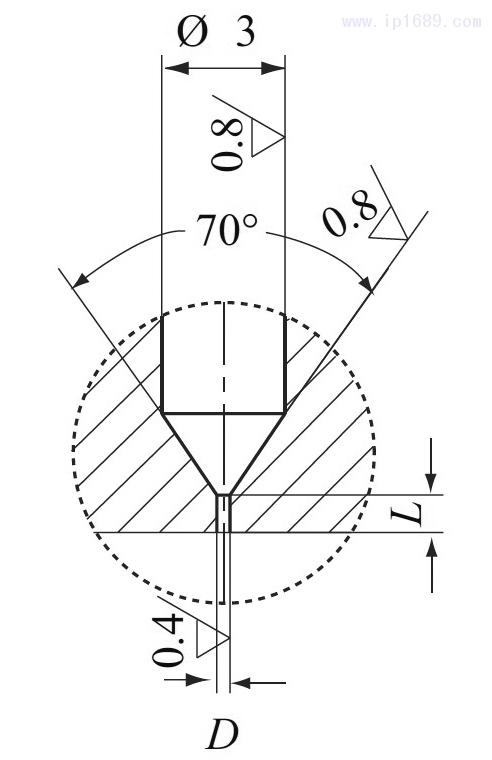
1.3幾何模型
根據課題組之前的研究表明[7],PE-UHMW/PE-HD共混物熔融紡絲過程中圓柱形擠出口模長徑比L/D為5,口模直徑D為0.6mm,口模收斂角為70°時,初生絲具有較好的擠出穩(wěn)定性,同時模具也容易被清理,因此選用該結構的噴絲板,其物理模型如圖1所示。
圖1擠出口模物理模型
2數(shù)值模擬
2.1三維模型建立
根據熔融紡絲擠出口模的物理模型,利用SolidWorks軟件建立三維模型,擠出口模三維模型示意圖如圖2所示。由于口模具有很好的對稱性,為減減少計算時間,方便分析,只對擠出口模的四分之一進行數(shù)值模擬。
圖2擠出口模三維模型
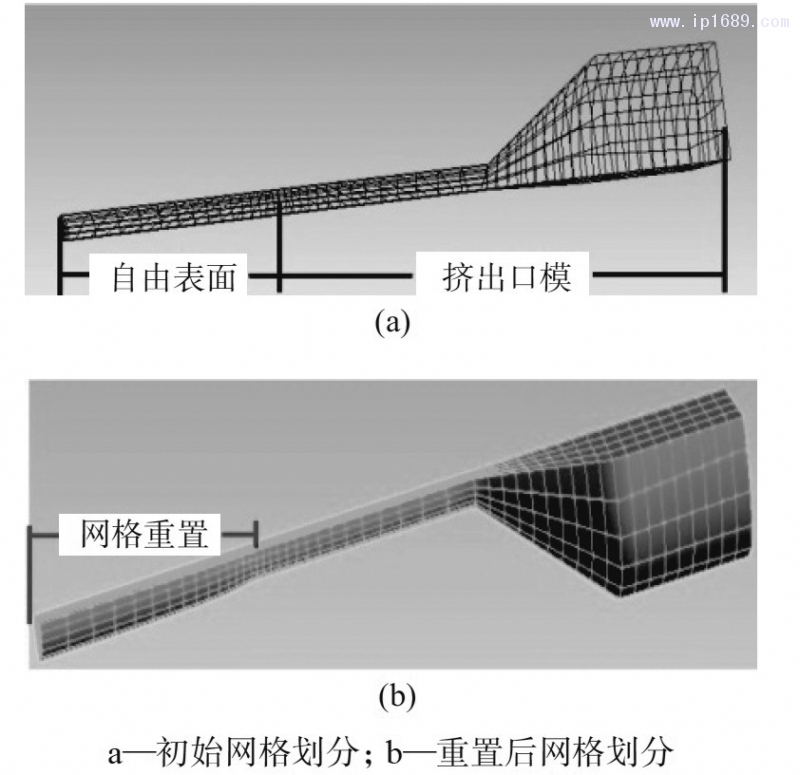
2.2網格劃分
將三維模型導入GAMBIT軟件,利用GAMBIT軟件對流道中的物料進行網格劃分,擠出物網格劃分的結果如圖3所示。
圖3擠出物網格劃分
圖3a顯示是初始網格劃分,共劃分單元3096個,節(jié)點4420個,邊界6個,鄰域2個。擠出過程中,物料在擠出口模后,會發(fā)生擠出脹大現(xiàn)象,因此模擬過程中會發(fā)生網格重置現(xiàn)象,如圖3b所示。
2.3材料參數(shù)和工藝參數(shù)
筆者主要研究擠出口模溫度和熔體泵轉速對PE-UHMW/PE-HD共混物熔融紡絲擠出脹大現(xiàn)象的影響,而實驗過程中擠出口模的溫度一般設定在280~310℃[15],熔體泵轉速設定在1~5r/min,因此模擬過程中溫度和轉速的變化也分別設定在這個范圍內。
利用哈克旋轉流變儀測定不同溫度下PE-UHMW/PE-HD共混物的各項性能,發(fā)現(xiàn)其零切黏
度、穩(wěn)定剪切黏性流動的無量綱材料參數(shù)、穩(wěn)態(tài)拉伸黏性流動的無量綱材料參數(shù)及純黏性部分與總黏度的比值幾乎不發(fā)生變化,分別為9000Pa·s,0.75,0.63,1/9;松弛時間隨著溫度的升高而減小,在不同溫度下,分別為0.0155,0.0112,0.0091,0.0062,0.0059,0.0055,0.0034s(280~310℃,每5℃測一次)。
2.4邊界條件
口模入口處:分別設定入口體積流率為5×10–8m3/s(1r/min),1.0×10–7m3/s(2r/min),1.5×10–7m3/s(3r/min),2.0×10–7m3/s(4r/min),2.5×10–7m3/s(5r/min)。
自由表面末端處:fn=fs=0;
口模內壁面:vn=vs=0;
初生絲表面:自由表面;
XY面和YZ面:對稱面。
vn表示法向速度,vs表示切向速度;
fn表示法向力,fs表示切向力。
2.5結果處理
綜合上述的物料參數(shù)、本構模型及邊界條件的設置,運用Polyflow進行數(shù)值計算,并利用該軟件的CFD-post功能進行結果處理,輸出擠出口模處的速度分布云圖和剪切速率分布云圖,分析擠出口模處的速度和剪切速率的變化趨勢,計算擠出脹大比等數(shù)據。
3結果分析
3.1速度場分析
共混物擠出口模的過程中,受到壁面無滑移條件的影響,口模中熔體流動速率的梯度分布是發(fā)生擠出脹大的重要因素,尤其是擠出口模徑向方向上的速度梯度。
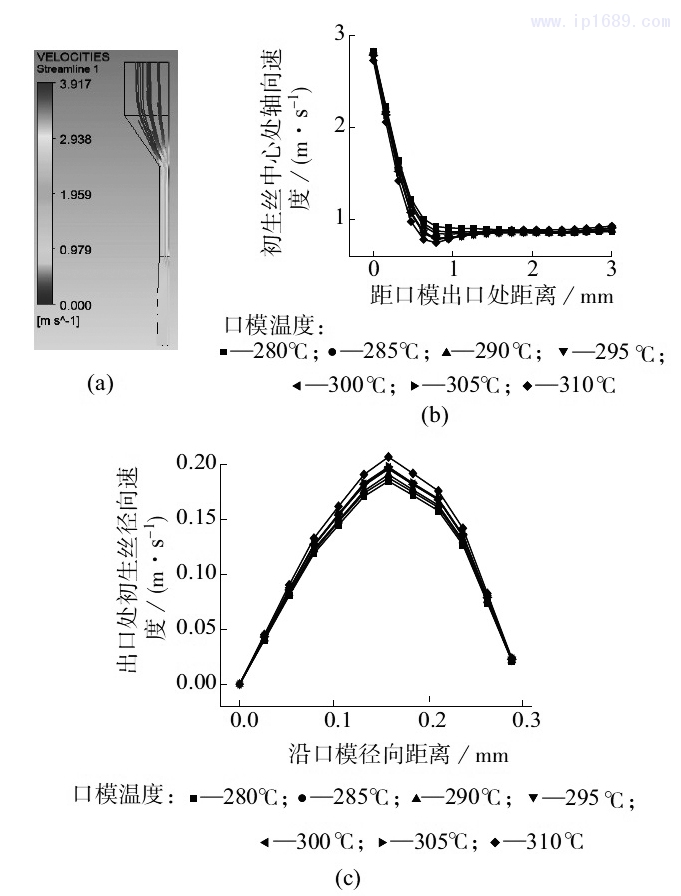
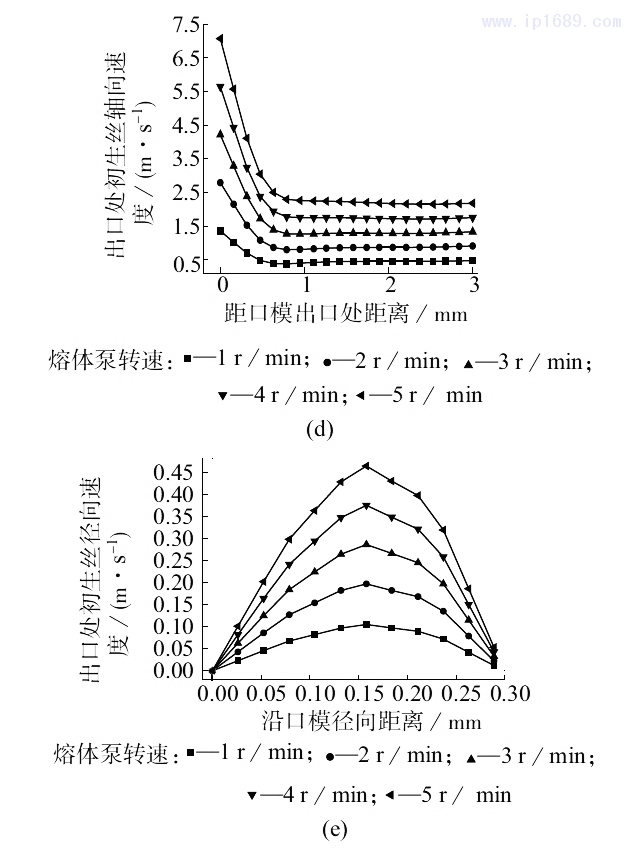
圖4是初生絲速度分布圖。口模內物料的軸向流動在失去壁面的束縛后,在口模外表現(xiàn)為軸向流動和徑向流動的疊加,從而產生明顯的擠出脹大現(xiàn)象(如圖4a所示)。不同加工溫度、不同熔體泵轉速下擠出口模的軸向速度和徑向速度分布變化情況如圖4b~圖4e所示。由圖4b和圖4d可以看出,不同溫度和轉速下,物料在流出擠出口模的瞬間,軸向方向的速度急劇降低,根據公式(2)中的動量方程可以分析得出,此時物料的流動由口模內的軸向流動轉變?yōu)閺较蛄鲃雍洼S向流動的疊加,如圖4c和圖4e所示,而且擠出口模溫度和計量泵轉速越高徑向速度越大,這主要是因為物料在口模中流動發(fā)生較高程度的取向,但是在離開口模后,失去口模的束縛,分子鏈發(fā)生解取向導致的彈性恢復現(xiàn)象;在離開口模一段時間后,分子鏈的解取向過程逐漸結束,徑向速度逐漸減小,幾乎變?yōu)?,此時物料的流動主要表現(xiàn)為軸向流動,即圖4b和圖4d中距口模出口0.5mm的位置,軸向速度急劇增大的現(xiàn)象,相應地,當徑向流動停止后擠出物的直徑就不再發(fā)生變化。
a—初生絲擠出口模過程中速度分布流線圖;
b—熔體泵轉速為2r/min時,不同口模溫度下初生絲中心處的軸向
速度分布;c—熔體泵轉速為2r/min時,不同口模溫度下出口處初
生絲徑向速度分布;d—口模溫度為300℃時,不同熔體泵轉速下初生
絲中心處的軸向速度分布;e—口模溫度為300℃時,不同熔體泵轉速
下出口處初生絲徑向速度分布
圖4初生絲速度分布圖
3.2剪切速率場分析
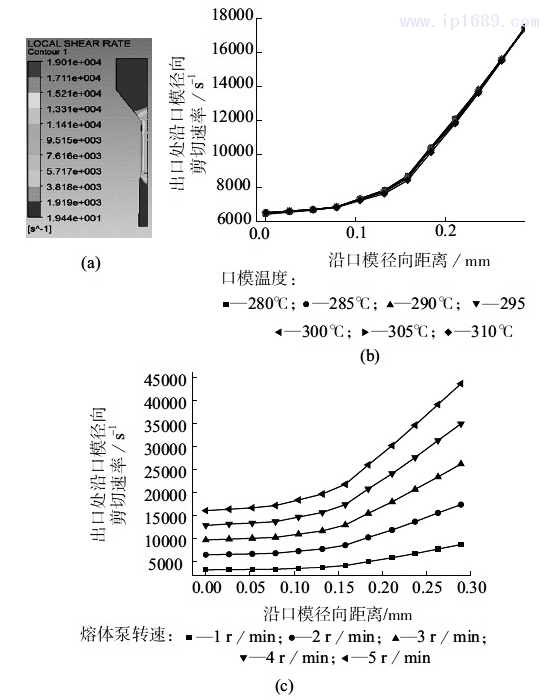
剪切速率的分布對分子鏈的取向和解取向過程有很大的影響。圖5為初生絲剪切速率分布圖。由圖5a可見,受到口模壁面的作用,徑向方向上的速度梯度較大,因此近壁面處物料受到的剪切速率最大,而在口模中心處,徑向方向上速度梯度小,口模中心處的剪切速率也減小。共混物料流出擠出口模后,物料的流動由口模內的軸向流動變?yōu)榭谀M獾妮S向流動和徑向流動的疊加,因此在擠出口模后,由于沒有了壁面的作用,初生絲外壁面處的剪切速率最小,但是受到徑向流動的影響,剪切速率由中心沿徑向方向逐漸減小,直至徑向方向上的速度變?yōu)?,剪切速率變成均勻分布。由圖5b和圖5c可看出,熔體泵的轉速不變時,隨著溫度的升高,最大剪切速率值沿徑向方向幾乎沒有發(fā)生變化,而在溫度不變時,隨著熔體泵轉速的增大,剪切速率在徑向方向上的分布成比例的增大,說明物料擠出口模的過程中速度梯度是影響剪切速率的主要因素。圖5c可以看出,熔體泵轉速越大,口模內最大剪切速率和最小剪切速率的差值越大,說明在離開口模后,沒有了壁面的約束,初生絲外壁面處剪切速率發(fā)生突變,但是中心處的剪切速率受到熔體的黏性作用,無法發(fā)生突變,因此剪切速率由梯度分布變?yōu)榫鶆蚍植嫉臅r間更長,擠出脹大現(xiàn)象更明顯。
a—初生絲擠出口模過程中剪切速率分布云圖;b—2r/min時,不同
口模溫度下出口處初生絲徑向剪切速率分布;c—300℃時,不同熔體
泵轉速下出口處初生絲徑向剪切速率分布
圖5初生絲剪切速率分布圖
3.3擠出脹大現(xiàn)象分析
擠出脹大現(xiàn)象一般利用擠出脹大比來表征,此處將流出擠出口模后的初生絲直徑和口模截面直徑之比定義為擠出脹大比,其計算方法如式(4)所示。
式中:B——擠出脹大比;
D——初生絲截面直徑;
D0——擠出口模截面直徑。
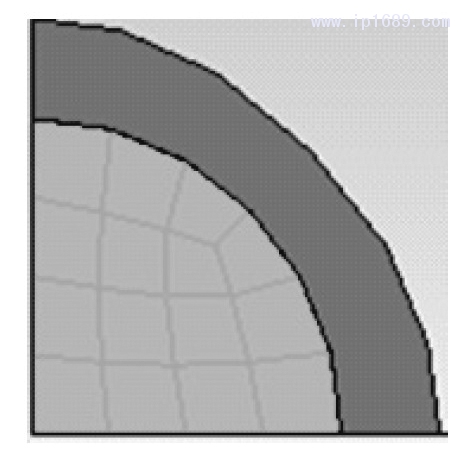
紡絲過程中的擠出脹大現(xiàn)象,直觀地表現(xiàn)為初生絲的直徑大于擠出口模的直徑,但是受到口模溫度、熔體泵轉速等工藝參數(shù)的影響,擠出脹大率會發(fā)生較大的變化。圖6為常見擠出脹大現(xiàn)象示意圖(1/4部分),其中內圈表示擠出口模,外圈表示初生絲。
圖6紡絲過程中擠出脹大現(xiàn)象示意圖
(1)口模溫度對擠出脹大比的影響。
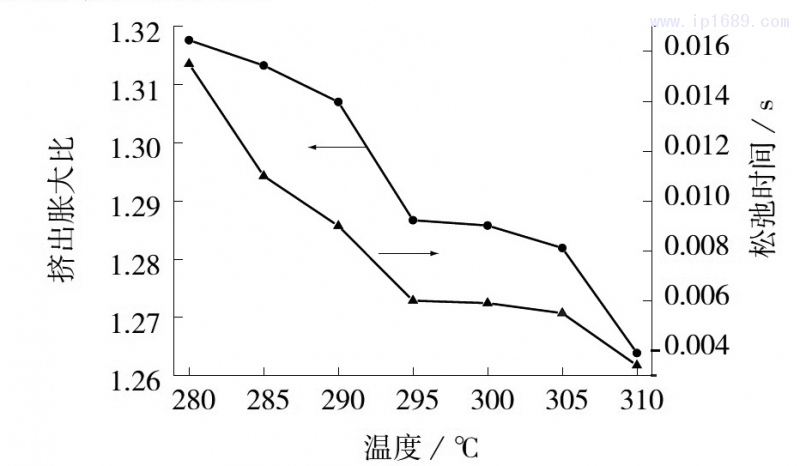
紡絲過程中,擠出口模的溫度是重要的工藝參數(shù),直接影響了物料的塑化狀況及分子鏈的取向及解取向狀況。圖7為初生絲擠出脹大比隨溫度變化。由圖7可見,隨著溫度的升高,初生絲的擠出脹大比呈下降趨勢,由280℃時的1.318降低到310℃的1.264,而且其減小趨勢與物料松弛時間的減小趨勢幾乎相當。這主要是因為在固定熔體泵轉速的情況下,物料流經擠出口模的時間是相同的,而松弛時間的減小會使口模中取向的分子鏈更快地解取向,即在口模內已經發(fā)生解取向;此時,聚合物分子鏈的運動能力明顯增大,熔體在流動過程中儲存的形變能明顯減小,彈性特性減弱,因此溫度越高,離開擠出口模的初生絲取向度越低,初生絲因解取向而發(fā)生彈性恢復的可能性越小,擠出脹大現(xiàn)象越不明顯,擠出脹大比越小。
圖7初生絲擠出脹大比隨溫度變化
(2)熔體泵轉速對擠出脹大比的影響。
熔體泵轉速對初生絲擠出脹大的影響主要表現(xiàn)為:熔體泵轉速的增加在一定程度上增大了口模徑向方向的速度梯度,從而增大了分子鏈的取向度;熔體泵轉速的增大使物料在擠出口模中的停留時間減小,使分子鏈在擠出口模內部發(fā)生解取向的可能性減小。
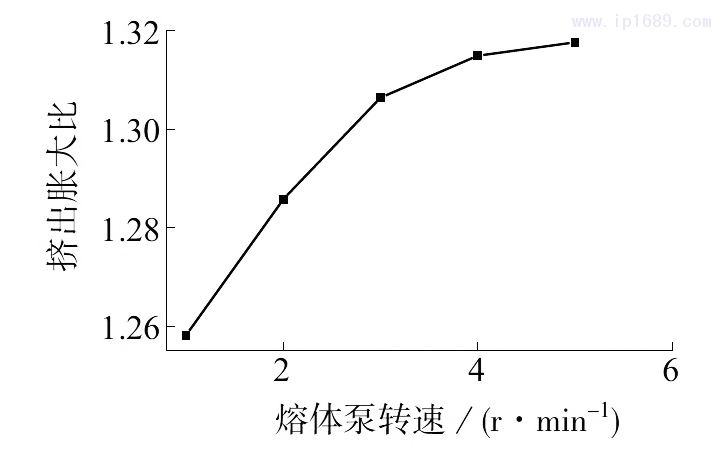
圖8為初生絲擠出脹大比隨熔體泵轉速變化。由圖8可見,隨著熔體泵轉速的增加,擠出脹大比逐漸增大,由轉速為1r/min的1.258增大到5r/min的1.318。擠出脹大比隨熔體泵轉速的增大而增大,這是因為:一方面,熔體泵轉速的增大使擠出口模徑向方向的速度梯度增大,如圖4e所示,微觀上,徑向速度梯度的分布增大了大分子鏈之間的內摩擦,內摩擦力使聚合物大分子鏈沿軸向方向取向,而且一定程度上速度梯度越大,內摩擦越大,分子鏈取向越明顯,離開口模后的回彈現(xiàn)象越嚴重,擠出脹大現(xiàn)象越明顯;宏觀上,徑向速度梯度的分布使口模內部物料受到的剪切速率增大,導致物料內部的法向應力差增大,擠出脹大比也增大。另一方面,熔體泵轉速的增大使物料在口模的停留時間減小,但是相同時間聚合物熔體的松弛時間是不變的,因此停留時間的減小使取向的分子鏈在口模中發(fā)生解取向的可能性減小,也就是說,在一定范圍內,熔體泵轉速越大,聚合物熔體在口模內的停留時間越短,聚合物大分子鏈在口模內的解取向程度越小,擠出口模后初生絲的回彈能力越強,擠出脹大現(xiàn)象越明顯,擠出脹大比越高。可以看出,速度梯度分布和停留時間對于PE-UHMW/PE-HD共混物熔融紡絲過程中的擠出脹大現(xiàn)象具有雙重作用。
圖8初生絲擠出脹大比隨熔體泵轉速變化
4結論
通過數(shù)值模擬分析PE-UHMW/PE-HD共混物紡絲過程中初生絲在不同溫度和不同熔體泵轉速下的物料流動狀況,可得到以下結論:
(1)在一定的溫度范圍內,初生絲的擠出脹大比隨擠出口模溫度的升高而降低,由1.318(280℃)減小到1.264(310℃);
(2)在一定的熔體泵轉速內,初生絲的擠出脹大比隨熔體泵轉速的增加而增大,由1.258(1r/min)增大到1.318(5r/min)。
參考文獻:
[1] 陳利民.超高分子量聚乙烯纖維在防彈材料上的應用[J].工程塑料應用,1995,23(6):31–34.
[2] 甄萬清,王慶昭,吳進喜,等.熔融紡絲法制備UHMWPE/MMT復合纖維的研究[J].合成纖維,2011,40(3):5–9.
[3] Liang J Z. Effects of extrusion conditions on die-swell behavior of polypropylene/diatomite composite melts[J]. Polymer Testing,2008,27(8):936–940.
[4] 黃偉,王曉春,楊中開,等.UHMWPE/聚烯烴共混物的性能及其熔融紡絲研究[J].合成纖維工業(yè),2015,38(6):43–48.
[5] 鄭艷超,楊中開,王曉春,等.熔紡PE-UHMW/聚烯烴共混體系及其纖維結構性能研究[J].北京服裝學院學報:自然科學版,2017(1):8–17.
[6] 王非.高密度聚乙烯改性超高分子量聚乙烯熔融紡絲的研究[D].北京:北京化工大學,2017.
[7] Doufas A K,Mchugh A J,Miller C. Simulation of melt spinning including flow-induced crystallization:Part I.Model development and predictions[J]. Journal of Non-Newtonian Fluid Mechanics,2000,92(1):27–66.
[8] 鄧小珍,柳和生,黃益賓,等.非等溫氣輔共擠出脹大的三維粘彈數(shù)值模擬[J].高分子材料科學與工程,2013,29(3):169–172.
[9] 李萍.聚合物氣體輔助擠出成型工藝及數(shù)值模擬[D].哈爾濱:哈爾濱理工大學,2010.
[10] 徐妍清.聚合物圓管氣輔擠出數(shù)值模擬與口模設計[D].南昌:南昌大學2015.
[11] 何建濤.塑料異型材氣輔共擠數(shù)值模擬與實驗研究[D].南昌:南昌大學,2014.
[12] 曹義.熔融紡絲組件熔體流動數(shù)值分析及其結構設計優(yōu)化研究[D].上海:東華大學,2006.
[13] Wang Fei,Liu Lichao,Xu Ping,et al. Crystal structure evolution of UHMWPE /HDPE blend fibers prepared by melt spinning[J].Polymers,2017,9(12):doi.org/10.3390/polym9030096.